浅析理解HashMap

发表于 | 分类 |
| 全文总计: 字
通过分析源码，看HashMap的底层原理

对于 HashMap 的日常开发使用，形如：

1
2
3
4
5
6
7
public static void main(String[] args) {
    HashMap<String, String> map = new HashMap<>();
    map.put("java", "java");
    map.put("python", "python");
    map.put("C++", "C++");
    map.put("C", "C");
}

其中最核心的问题是，这个 HashMap 容器怎么就能把 k-v 保存起来，并且还能通过 key 来获取呢？其中最核心的方法就是在于如何插入数据，这个put()怎么就顺利将数据存入集合，有没有元素数量极限呢？容器初始化的时候是无限大，还是有个固定值，还是先有个固定值，不够装的时候再扩容呢？这些问题， 都是本文要探讨的问题。

1. HashMap 容器本质

1.1 数组 + 链表 / 红黑树

在 JDK1.7 中，HashMap 底层采用的是数组+链表的形式存储数据。在 JDK1.8 中，HashMap 底层采用的是数组+链表/红黑树的形式存储数据（当达到链表长度一定阀值的时候，链表会转成红黑树）。

在 JDK1.7 中，用户保存的数据是以 k-v 的形式存进容器，容器根据 key 的 hash 值进行计算，得到当前数据要保存到数组的中索引位置，如果获得的所以位置一样，那么新来的元素会存在链表的头部。

通过上述的描述，可以自己纯手工撸制一个属于自己的 HashMap 容器，值得注意的是，容器对外暴露的接口就是个put(k,v)方法，但是为了能实现链表结果，那么就需要将用户的数据进行封装成链表节点，因此需要自定义一个链表节点对象，该对象初步应该有用户的 k-v 数据属性，还要有可以指向下一个链表节点的属性。

1.2 伪代码实现

每一个 key 在存入 HashMap 之前，要对key进行 hash 计算，并对数组长度取模等计算，得到要存储的数组索引下标：

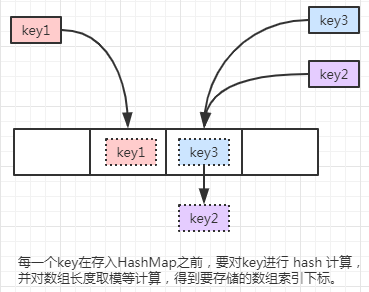
先模拟 key 生成 hash 值，并对数组长度进行取模计算：

1
2
3
4
5
6
7
8
9
String[] keys = {"java", "python", "C++", "C"};

int arrayLength = 8;

for(String key : keys) {
    int hashCode = key.hashCode();
    int index = hashCode % (arrayLength - 1);
    System.out.println(String.format("%s %d  %d", key , hashCode, index));
}

输出结果：

1
2
3
4
java 3254818  0
python -973197092  0
C++ 65763  5
C 67  4

从上述输出结果可以看出，”java” 和 “python” 主键得到的要存储的索引位置是一样的，那么它们都会存储在数组索引下标为 0 的位置。

其中 “python” 是后存进来的，在 JDK 1.7 中，会插入到链表的头部，也就是当前数组索引所保存的数据对象一定是当前链表元素中最新（最后插入）的元素。

对于上述，通过 key 计算 hash 值并对数组长度取模得到下标索引的伪代码：

1
2
3
4
5
6
7
8
9
10
int hashCode = key.hash();
index = hashCode % (table.size() - 1);
table[index] = new Node(key, value, table[index]);

// 其中 Node 为链表节点对象
Node<K,V>{
    K key;
    V value;
    Node<K,V> next;
}

注意的是：每次要插入的节点的下一个指针，指向当前要插入的数组的索引位置的节点，就能实现新来的节点在链表的头部，即当前数组索引位置的元素就是最新的插入元素。

2. 自定义 HashMap

2.1 设计思路

自定义一个MyHashMap，实现Map接口，实现如下方法，在 IDEA 工具中按Alt + 7快捷键显示当前类的所有方法：

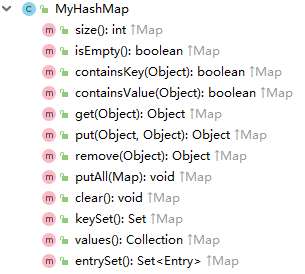
本文只为了研究理解 HashMap 的核心原理，暂只实现部分方法（也就是不实现 Map 接口）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public class MyHashMap<K, V>  {

    /**
     * 当前容器中的元素个数
     * @return
     */
    public int size() {
        return 0;
    }

    /**
     * 获取数据
     * @param key
     * @return
     */
    public Object get(K key) {
        return null;
    }

    /**
     * 插入元素
     * @param key
     * @param value
     * @return
     */
    public Object put(K key, V value) {
        return null;
    }

}

为了保证自定义的 HashMap 能模拟数组+ 链表的形式，就需要自定义一个链表的节点对象，数组的类型就是该链表节点对象类型：

1
2
3
4
5
class MyEntry<K, V> {
    K key;
    V value;
    MyEntry<K,V> next;
}

2.2 容器基本属性设计

有了上述的基本链表节点结构之后，就可以根据 HashMap 的底层容器逻辑，设计出类似的存储结构了：在自定义的容器中，设计一个默认的链表节点数组，并设置其默认数组大小：

1
2
3
4
5
6
7
8
9
10
11
12
// 记录容器元素的个数
private int size = 0;

private static final int DEFAULT_CAPACITY = 8;

// 数组+链表的数据结构
private MyEntry[] table;

public MyHashMap() {
    // 默认的链表节点数组
    this.table = new MyEntry[DEFAULT_CAPACITY];
}

通过这样几个属性的定义和构造函数的设计，就能实现 HashMap 的存储结构了。

2.3 插入元素代码实现

此时，最简单版本的插入元素逻辑就可以实现出来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * 插入元素
 * @param key
 * @param value
 * @return
 */
public Object put(K key, V value) {

    int hashCode = key.hashCode();
    int index = hashCode % this.table.length;
    addEntry(key, value, index);
    
    // 容器元素个数统计自增，避免每次获取元素个数要遍历整个容器，提升效率
    this.size++;

    return null;
}

/**
 * 添加节点
 * @param key
 * @param value
 * @param index
 */
private void addEntry(K key, V value, int index) {
    this.table[index] = new MyEntry(key, value, this.table[index]);
}

在 Map 接口中要求，插入元素要返回一个 Object 对象，如果要插入元素的 key 是个新的 key，即原始容器中不存在这个 key，那么就返回当前要插入元素的 key 对应的 value 。如果要插入元素的 key 是个已存在的，那么将新的 value 覆盖掉旧的 value，并返回旧的 value。通过查看 JDK1.7 的源码可以验证：

因此可以进一步完善自定义的插入元素方法实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
/**
 * 插入元素
 * @param key
 * @param value
 * @return
 */
public V put(K key, V value) {

    int hashCode = key.hashCode();
    int index = hashCode % this.table.length;

    // 遍历链表，如果发现当前要插入的元素已存在，更新 value，返回旧的 value
    for(MyEntry<K,V> myEntry = this.table[index]; myEntry!= null; myEntry = myEntry.next) {
        if(key != null && key.equals(myEntry.key)) {
            V oldValue = myEntry.value;
            myEntry.value = value;
            return oldValue;
        }
    }

    addEntry(key, value, index);

    // 容器元素个数统计自增
    this.size++;

    return null;
}

2.4 获取元素代码实现

由此，遍历链表的操作，在 get 操作的时候也要进行：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
/**
 * 获取数据
 * @param key
 * @return
 */
public Object get(K key) {
    int hashCode = key.hashCode();
    int index = hashCode % this.table.length;

    for(MyEntry<K,V> myEntry = this.table[index]; myEntry!= null; myEntry = myEntry.next) {
        if(key != null && key.equals(myEntry.key)) {
            return myEntry.value;
        }
    }

    return null;
}

2.5 测试自定义容器

测试自定义 HashMap 的插入元素操作：

1
2
3
4
5
6
7
8
public static void main(String[] args) {
    MyHashMap<String, String> map = new MyHashMap<>();

    for(int i = 0; i< 10; i++) {
        map.put("java"+i, ""+i);
    }
    map.get("java3");
}

通过 debug 查看容器结构，可以看到：其中一些已经形成链表，并且后插入的元素在链表的头部：

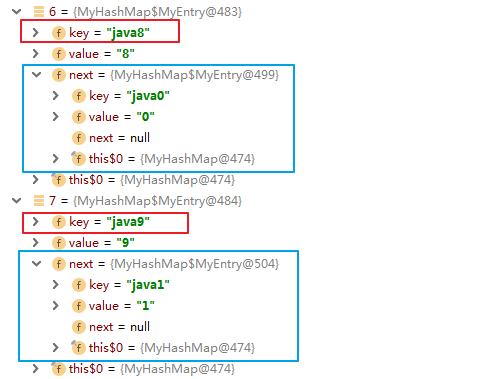
3. JDK 1.7源码分析

3.1 HashMap 基本属性

查看 JDK 1.7 中的 HashMap 源码，首先看看其中的重要属性值，包括默认容器大小，最大最小容器大小，扩容因子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public class HashMap<K,V> {

    /**
     * The default initial capacity - MUST be a power of two.
     * 默认初始化容器大小为16，大小必须是 2 的次幂
     */
    static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; // aka 16

    /**
     * The maximum capacity, used if a higher value is implicitly specified
     * by either of the constructors with arguments.
     * MUST be a power of two <= 1<<30.
     * 容器大小限制，取值范围为：2 - 2的30次方的 2 的次幂数
     */
    static final int MAXIMUM_CAPACITY = 1 << 30;

    /**
     * The load factor used when none specified in constructor.
     * 默认容器扩容因子，也就是当容器中的元素数量到达一定阀值的时候，需要对容器进行扩容
     */
    static final float DEFAULT_LOAD_FACTOR = 0.75f;
}

上述重要属性已经在注释中进行了说明，不再赘述。

在 HashMap 构造函数中，有个很特别的方法，这个方法会将用户指定的容器大小，进行计算，保证容器大小为 2 的次幂：

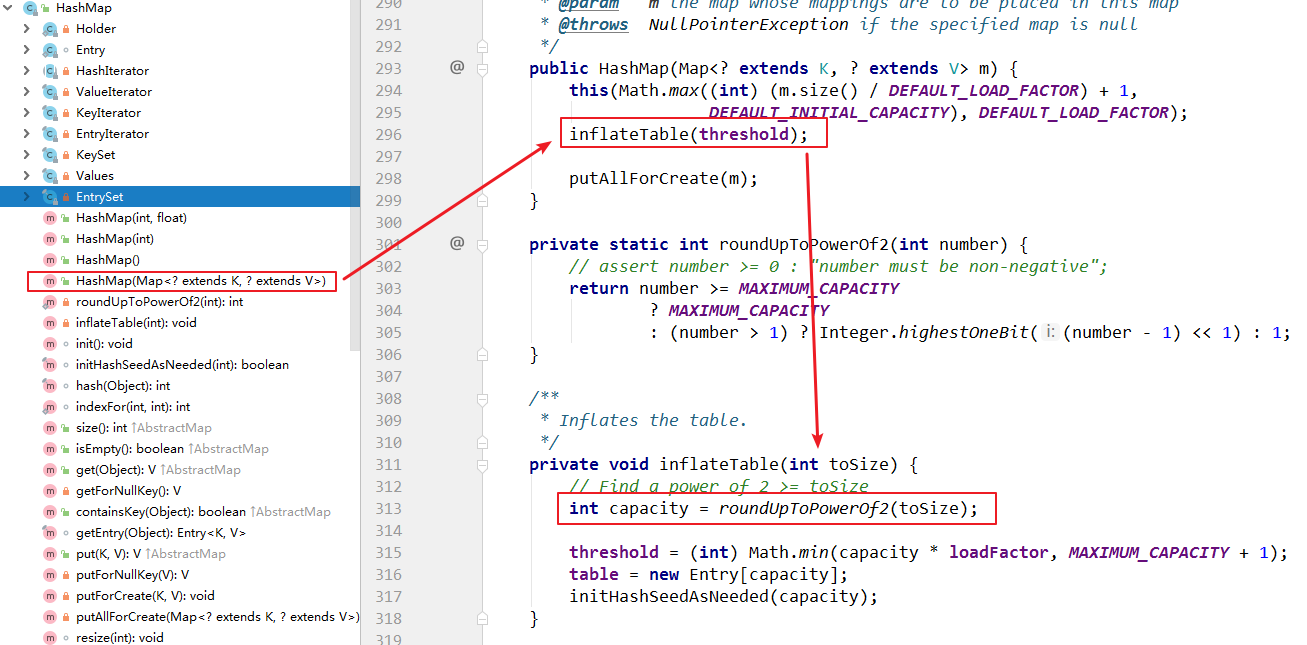
在roundUpToPowerOf2(toSize);方法的注释也说明了该方法就是要找到：大于或等于指定数值的 2 的次幂的值。

通过源码可以知道，为什么 HashMap 强制要求容器大小为 2 的次幂数呢？

3.2 插入元素

再次细致分析插入元素方法：

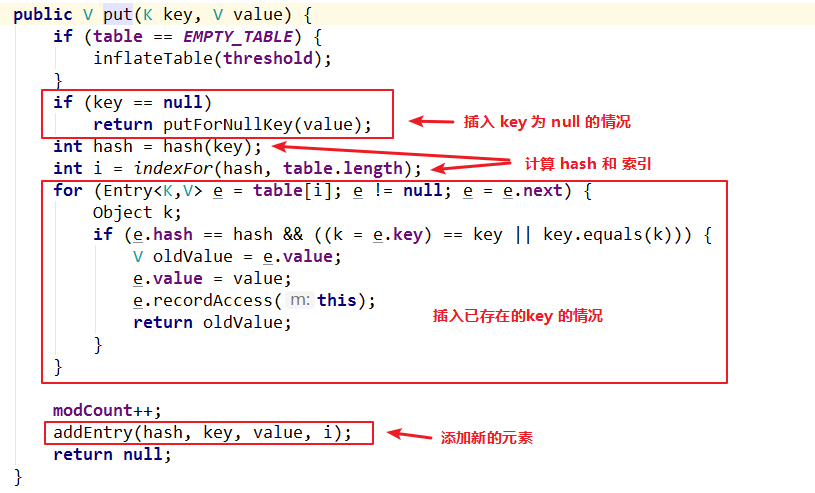
通过源码可以分析，插入元素分为了四个步骤：

  • 判断 key 是否为 null，如果是则进行空值插入处理。
  • 计算 key 的 hash 值，并通过这个 hash 值得到要插入的数组索引。
  • 遍历要插入的位置的链表，看是已经存在当前 key 了。已存在则更新当前 value 并返回旧的 value。
  • key 是全新的元素，则进行插入操作，也就是在链表中添加新的节点。

因此对于插入元素的源码分析，可以分为上述的四个模块来分析：

3.2.1 计算 key 要插入的索引

新来看看hash() 和indexFor()方法：

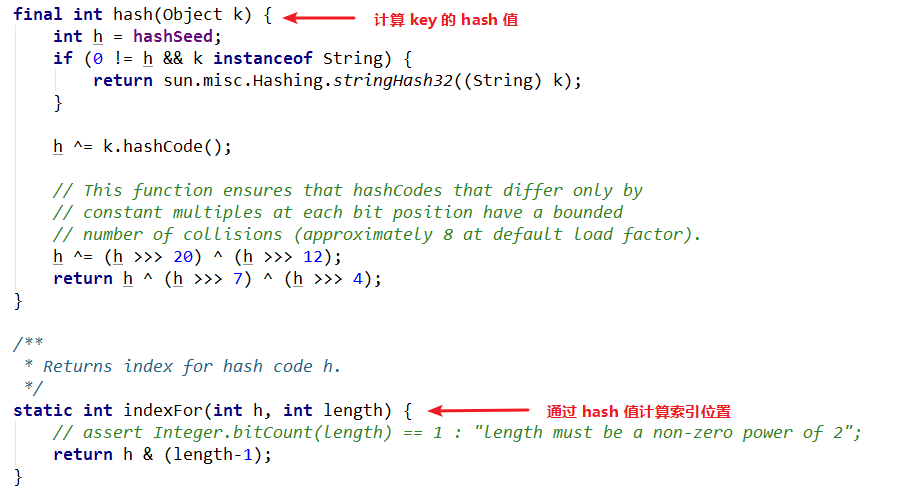
通过源码可以看出，原生的 hash 值经过了右移操作，处理过的 hash 值和数组长度并非取模操作， 而是进行了按位与操作。

为什么要按位与操作？

由于数组长度限制必须为 2 的次幂，因此数组长度取值只可能为：2，4，8，16，32，……，这些数字的二进制分别为：

| 十进制 | 二进制 |
| —— | —— :|
| 2 | 0000 1000 |
| 4 | 0000 0100 |
| 8 | 0000 1000 |
| 16 | 0001 0000 |
| 32 | 0010 0000 |

当上面这些数字减 1 的时候，对应的二进制为：

| 十进制 | 二进制 |
| —— | —— :|
| 1 | 0000 0001 |
| 3 | 0000 0011 |
| 7 | 0000 0111 |
| 15 | 0000 1111 |
| 31 | 0001 1111 |

按位与操作：按位与处理两个长度相同的二进制数，两个相应的二进位都为1，该位的结果值才为1，否则为0。如：0101 AND 0011 = 0001

由于长度减 1 之后的数值就是索引能取到的最大索引位置，对应的二进制低位数都是 1，因此保证了低位进行与操作的时候，保持了 hash 值的低位值，高位全部被转成了 0 ，也就满足了 hash 无论多长，通过与操作，都能落在数组索引范围内：

上述描述很抽象，用下图例子辅助说明，假设容器大小为 16，那么对应的二进制如下：

其他 2 的次幂值均满足，该值减 1 之后，低位都是 1，再和其他任意数值进行与操作的时候，低位保留，高位全部变为 0，因此与操作之后，一定是一个 0 - （2的次幂-1）的值，这个取值范围就是数组索引的范围。

为什么要右移和异或？

明白了上述为什么要与操作，那么 hash 值右移和异或操作的目的就很一目了然，右移操作，就是保留高位，去掉低位。在进行与操作的时候，就是拿 hash 值的高位进行与操作，得到索引值。目的就是增加元素的散列性，不同 key 的hashCode 的低位存在冲突的可能性更大的一些，而高位存在冲突的可能性小一些，因此要右移和异或操作。

3.2.2 插入新元素

插入新元素要看addEntry()方法：

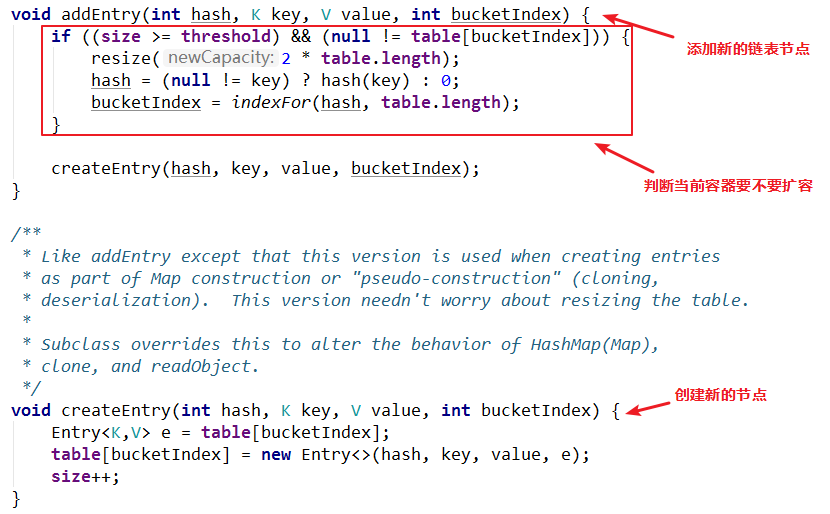
对于新增节点的逻辑，就是和 2.3 小节的实现思路是一致的，不再赘述。

对于扩容机制单独开一个小节分析，这里只分析插入元素相关的代码逻辑。

3.2.3 插入旧元素

对于旧元素的插入，在 2.3 小节中也已经讲述，这里不再赘述。

3.2.4 插入null

插入key 为 null 的情况，要看putForNullKey()方法：

通过源码可以分析得出：HashMap 是可以存入 null 元素的，并且存储在数组索引为 0 的位置。

3.3 扩容机制

在新增链表节点的addEntry()方法中可以看到：

1
2
3
4
5
6
7
8
9
void addEntry(int hash, K key, V value, int bucketIndex) {
    if ((size >= threshold) && (null != table[bucketIndex])) {
        resize(2 * table.length);
        hash = (null != key) ? hash(key) : 0;
        bucketIndex = indexFor(hash, table.length);
    }

    createEntry(hash, key, value, bucketIndex);
}

判断要扩容的条件是两个，而不是仅仅达到扩容阀值的时候才扩容，还满足当前要插入的元素在要插入的位置已经有元素了才扩容。也就是说，即使元素个数到了扩容阀值，如果当前元素进来，插入到数组某个空的”插槽”中，那么不会扩容。

扩容后的数组长度是原来数组长度的俩倍。重点来研究一下resize()方法：

要搞清楚 HashMap 的扩容，核心就是搞懂transfer()方法，如何实现旧表中的元素转移到新表中：

从上图代码可知：转移步骤如下：

  • 依次遍历旧表中的元素，直到所有的旧元素全部转移到新表中才结束

  • 将当前元素的下一个元素临时保存住，以备用

  • 重新计算当前元素插入到新表的索引

  • 将当前元素的下一个元素指向新表的索引位置元素

  • 将新表的元素设置为当前新插入的元素

  • 将临时保存的下一个元素取出，继续上述循环操作

3.4 扩容机制引发的多线程并发问题

HashMap 在并发环境下多线程 put 后可能导致 get 死循环，具体表现为 CPU 使用率100%，问题根源在于扩容机制中的旧元素转移到新表中。

首先分析单线程情况下的扩容情况：

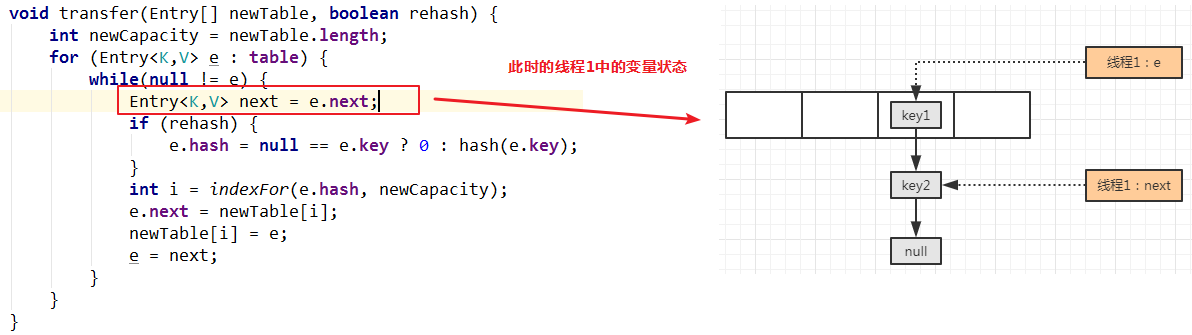
一般情况下，refreah 值为 false ，因此不是扩容机制分析的重点，不作分析。

重新计算索引位置，并将当前线程变量 e 的 next 指向新表中的索引位置元素：

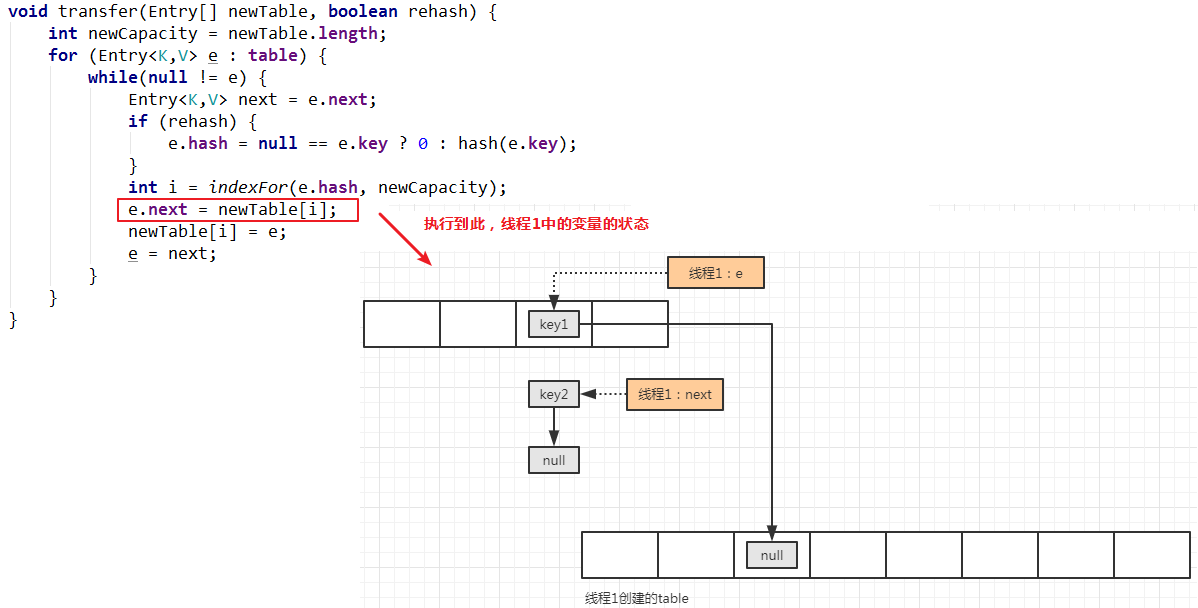
下一步就是将插入的元素放置到链表的头部，并保存在新表索引的位置：

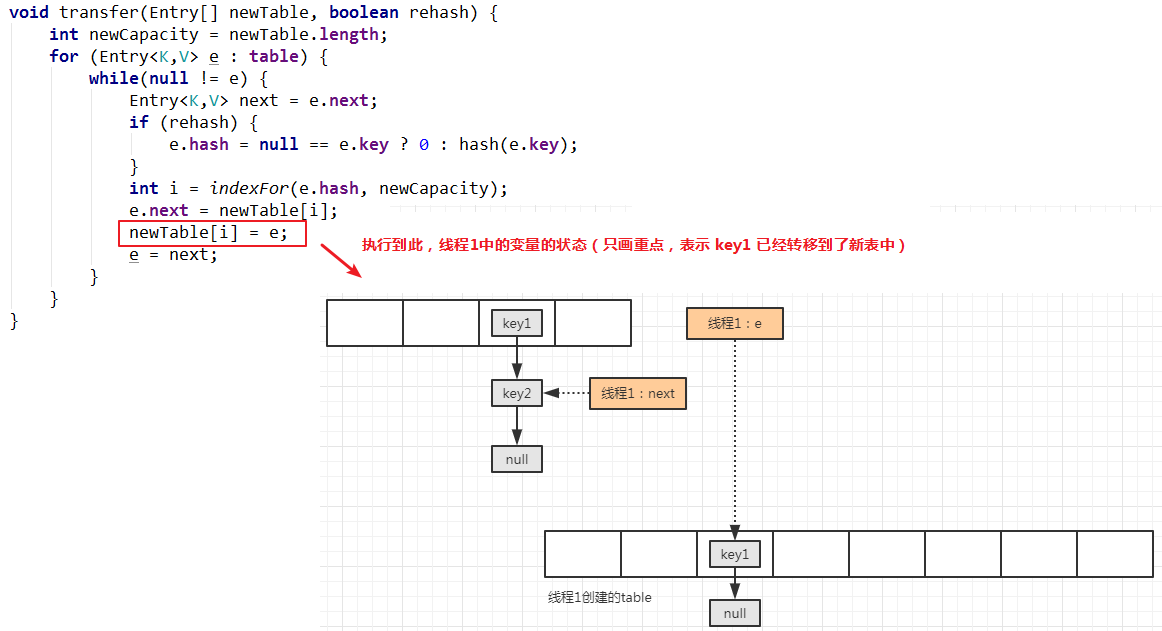
第一个要转移的元素已经移动完毕，将最开始临时保存的这个已转移之前的下一个元素取出，继续新的移动操作：

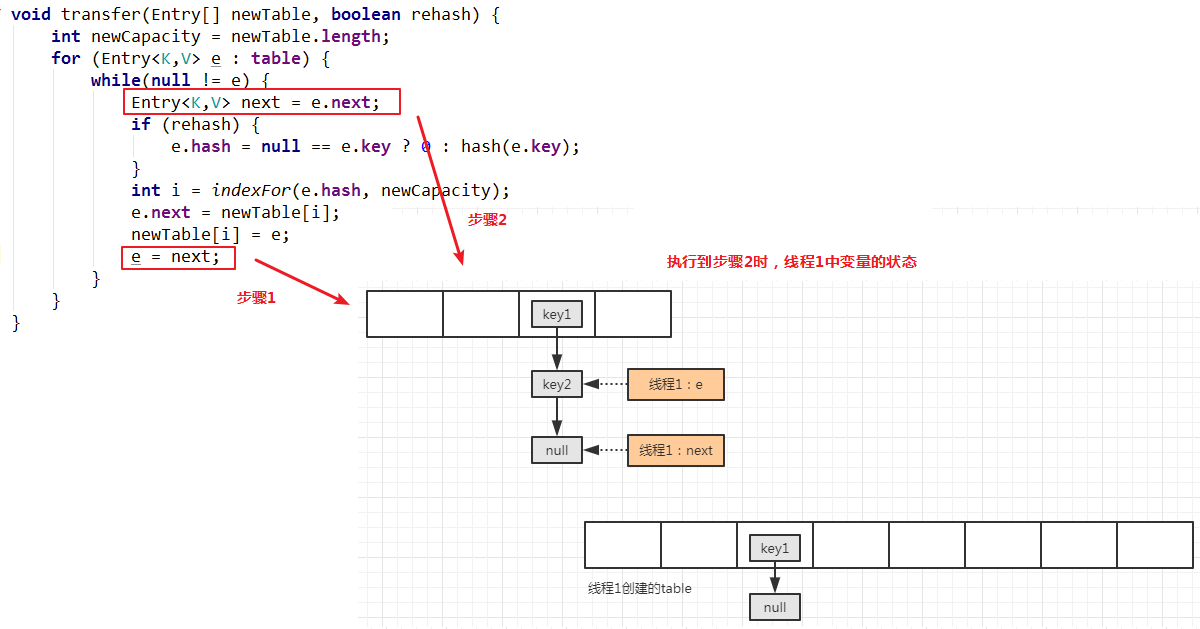
移动第二次，当移动完毕时：

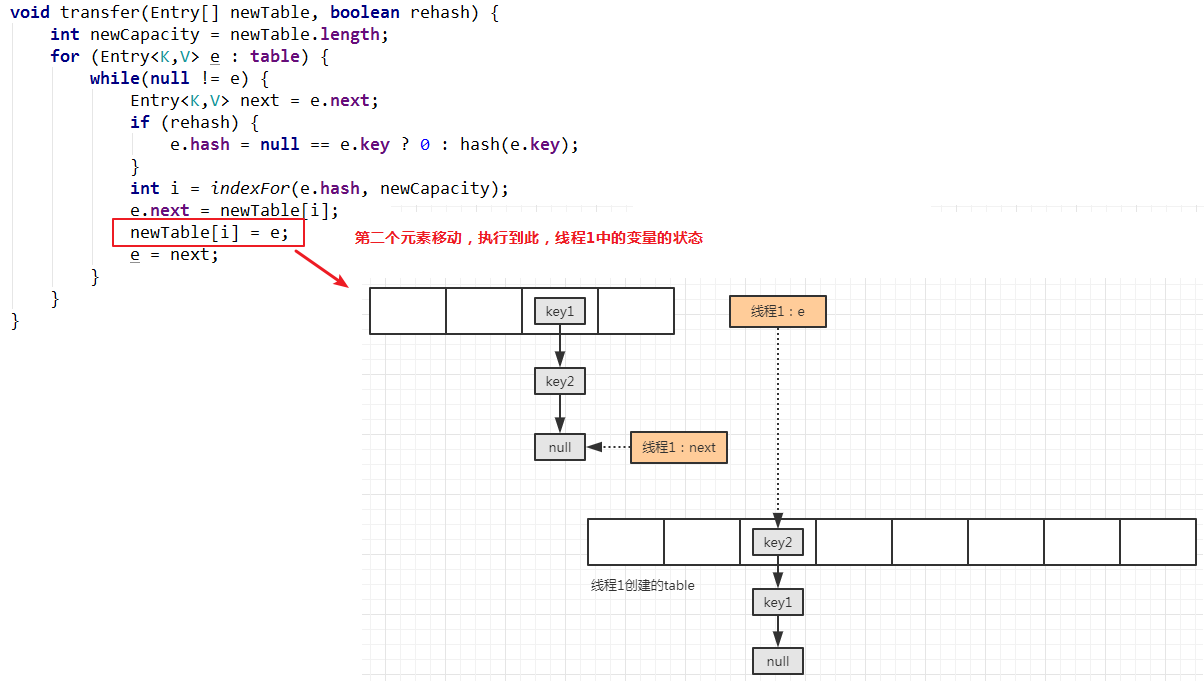
从上述一个元素的移动操作过程可以看出，旧表的链表顺序的 key1 -> key2 -> null，存进新的链表中的顺序的倒序的，也就是 key2 -> key1 -> null。

多线程问题分析

由于多线程都共享旧的表，新的线程同时 put 操作的时候，可能都会触发扩容操作，那么两个线程均为创建一个新的表，假设此时线程2 在 put 操作过程中莫名地停顿了一下，线程1 继续顺畅执行。

在两个线程都需要扩容的时候，都创建好了新表，都执行到了移动元素的方法中，此时两者的线程变量状态为：

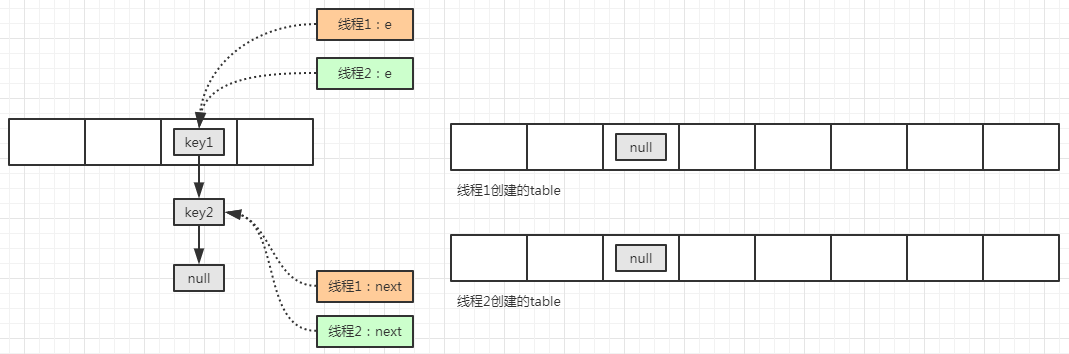
由于莫名的原因，线程 2 停顿了一下，线程1 正常执行完毕移动操作：

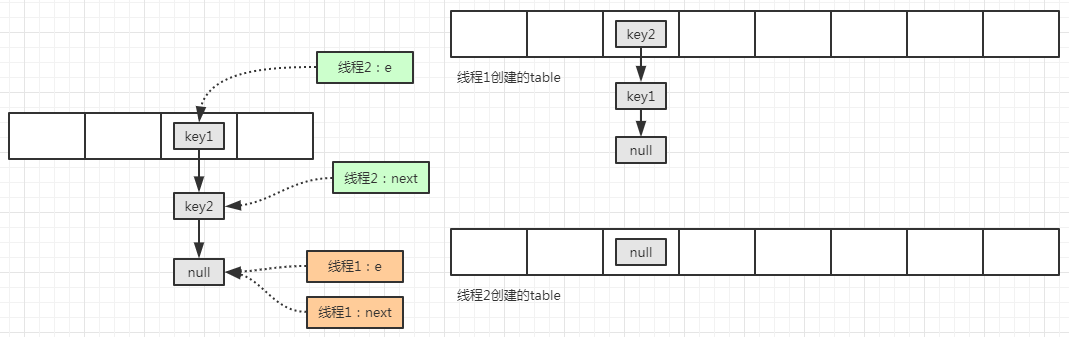
上图只是个理想状态，因为线程2中的变量 e 指向的永远是 key1 对应的内存地址，变量 next 指向的是 key1 的 next 变量指向的内存地址，因此正确的状态图为：

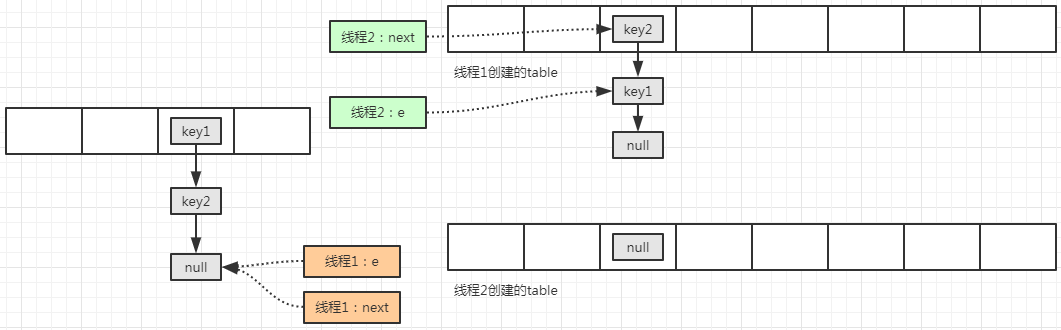
此时，线程2 继续执行移动元素操作：

将线程2 的 e 变量所指向的元素移动到线程2 创建的 table 中，并将线程2 的 next 变量所指向的元素赋值给线程2的 e 变量，此时的状态图为：

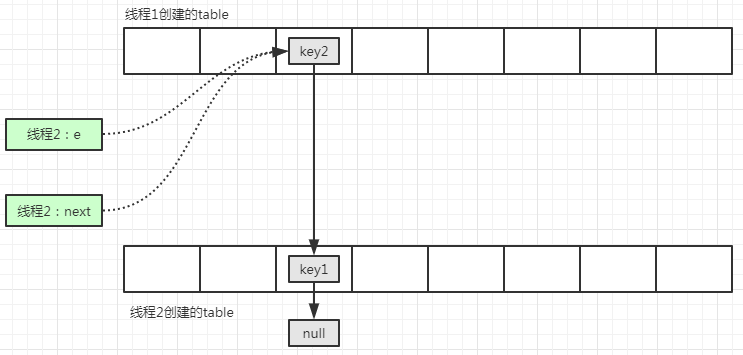
线程2 再次执行下一次循环，此时变量 next 指向的 线程2 的新表的索引位置：

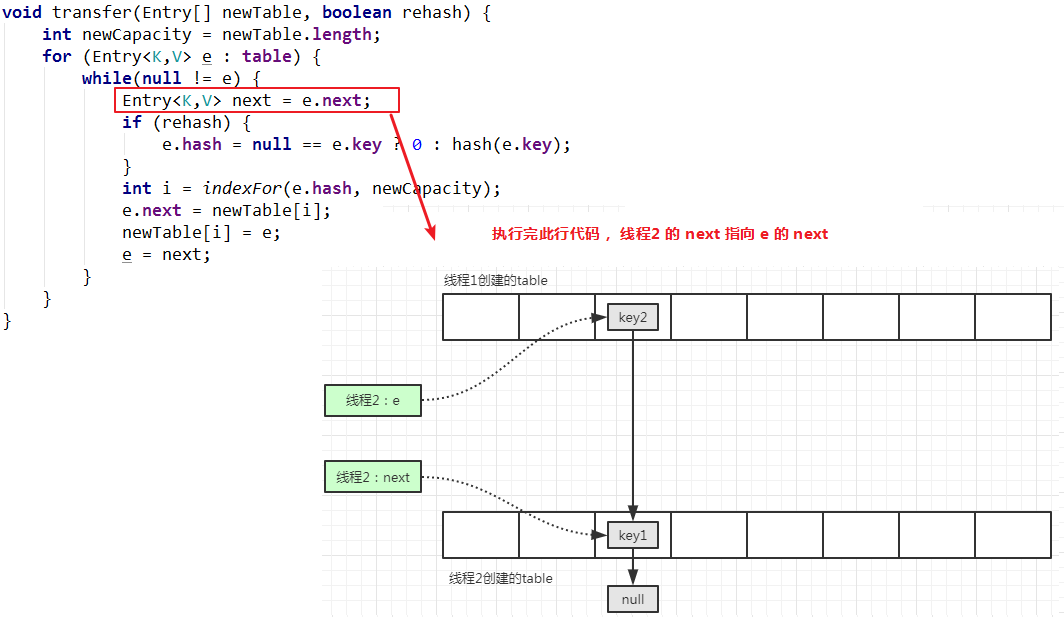
注意，此时要计算变量 e 对应的元素的索引，还是在线程2 的新表中的 key1 所在位置，当执行e.next=newTable[i]的时候，会发现一个问题：e 指向的元素是线程1 新表中的 key2，而 key2 的下一个元素就是指向线程2 新表中的索引位置，也就是 newTable[i] 指向的内存地址，此行代码执行无效。

继续执行代码新元素插入到链表头部的操作：

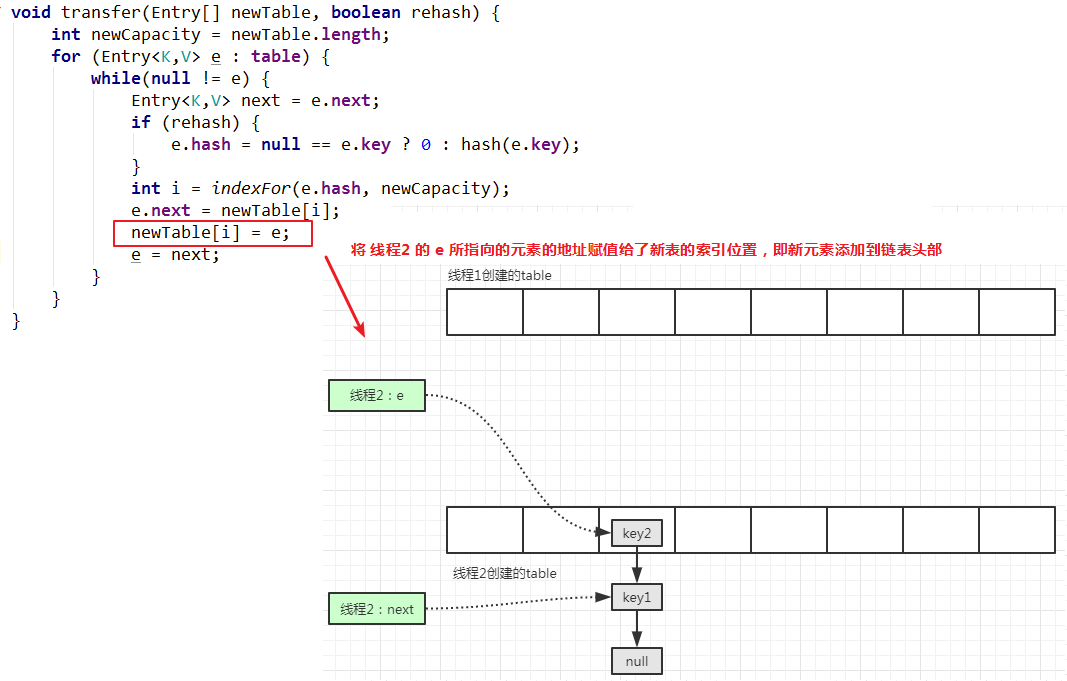
继续下一次循环：

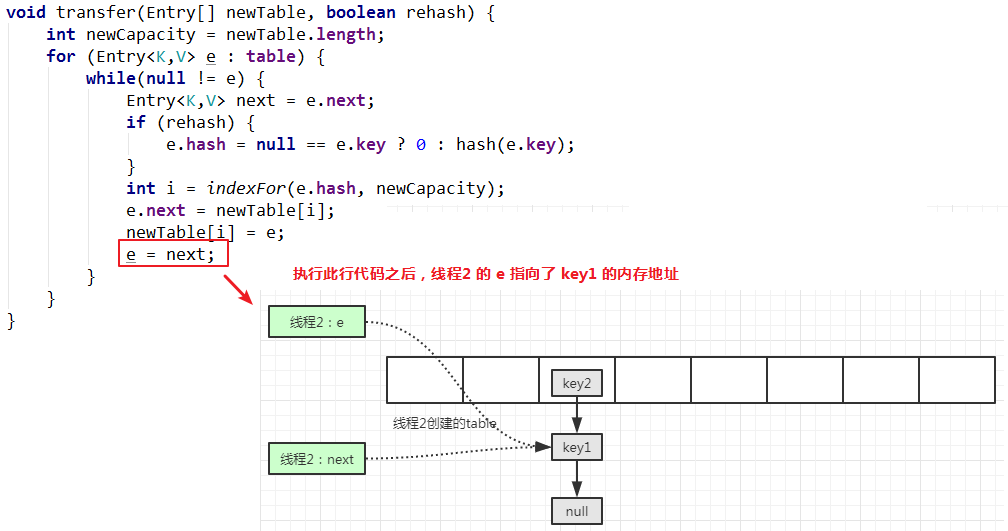
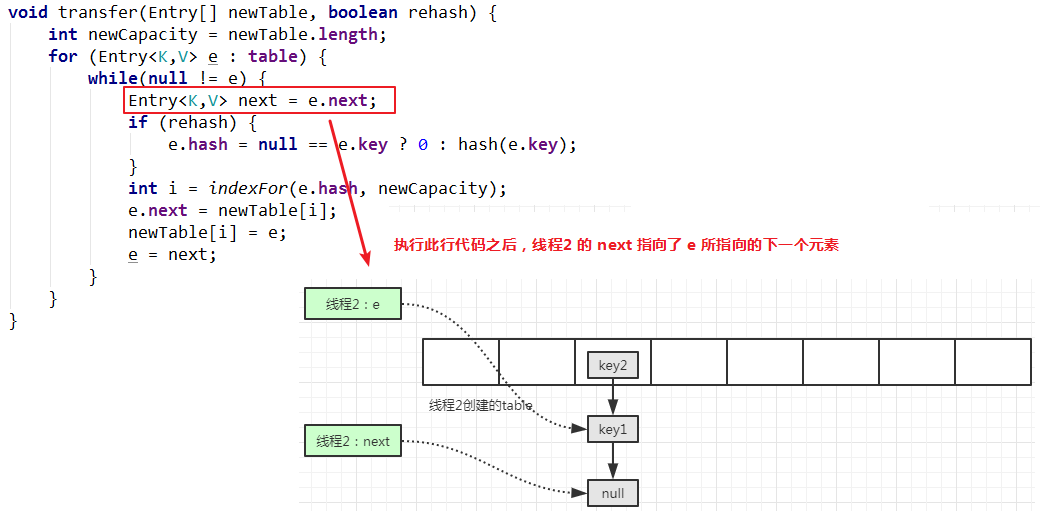
继续执行代码：

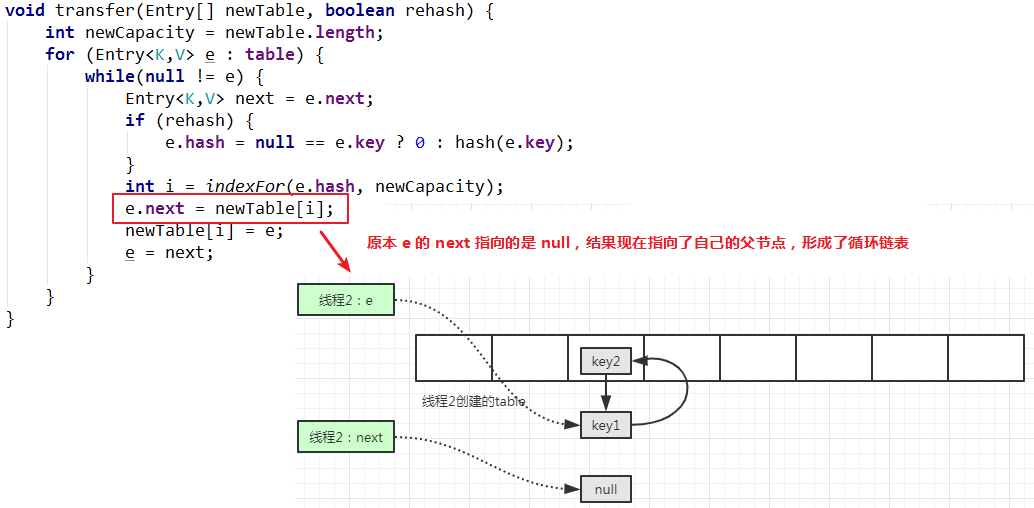
幸好，在 JDK1.8 中已经避免了这个问题，因为在 JDk 1.8 中，元素转移到新表的时候，是保持原有顺序的，因此不会出现产生这种循环链表的情况。

3.5 ConcurrentModificationException 异常

编写一个测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public static void main(String[] args) {
    try {
        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        map.put(1, 1);
        map.put(2, 2);
        map.put(3, 3);
        Set<Integer> set = map.keySet();
        for(Integer k : set){
            map.remove(k);
        }
    } catch (Exception e) {
        e.printStackTrace();
    }
}

运行时会报java.util.ConcurrentModificationException异常

如果换成 iterator 遍历 map，那么就不会报异常：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
try {
    Map<Integer, Integer> map = new HashMap<Integer, Integer>();
    map.put(1, 1);
    map.put(2, 2);
    map.put(3, 3);
    Set<Integer> set = map.keySet();
    Iterator<Integer> it = set.iterator();
    while (it.hasNext()) {
        Integer v = it.next();
        it.remove();
        System.out.println(map);
    }
} catch (Exception e) {
    e.printStackTrace();
}

4. JDK 1.8 源码分析

JDK 1.8 中当链表长度达到一定阀值的时候，就会将链表转成红黑树，为什么是红黑树，而不是平衡二叉树或者其他树结构，也是需要浅析一下：

4.1 三种树结构

打旧金山大学的开数据结构可视化网站：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

分别比较二叉树、平衡二叉树（AVL）、红黑树的结构：

4.1.1 平衡二叉树（AVL）

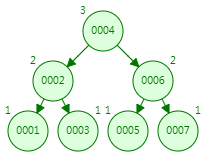
平衡二叉树或为空树，或为如下性质的二叉排序树：

1）左右子树深度之差的绝对值不超过1

2）左右子树仍然为平衡二叉树

平衡因子BF = 左子树深度－右子树深度

平衡二叉树每个结点的平衡因子只能是1，0，-1。

若其绝对值超过1，则该二叉排序树就是不平衡的。

4.1.2 红黑树（RBT ）

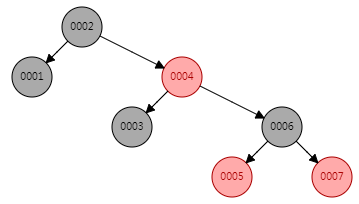
AVL 是严格平衡树，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多；

红黑是弱平衡的，用非严格的平衡来换取增删节点时候旋转次数的降低；

所以简单说，搜索的次数远远大于插入和删除，那么选择 AVL 树；如果搜索，插入删除次数几乎差不多，应该选择RBT树。

红黑树上每个结点内含五个域，color，key，left，right，p。如果相应的指针域没有，则设为NIL。
一般的，红黑树满足以下性质，即只有满足以下全部性质的树，我们才称之为红黑树：
1）每个结点要么是红的，要么是黑的。

2）根结点是黑的。

3）每个叶结点，即空结点（NIL）是黑的。

4）如果一个结点是红的，那么它的俩个儿子都是黑的。

5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

4.1.3 二叉树搜索树（BST）

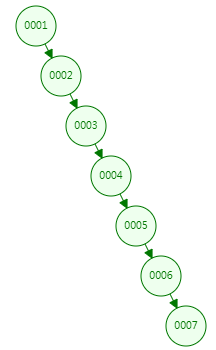
所有非叶子结点至多拥有两个儿子（Left和Right）；

所有结点存储一个关键字；

非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

总结下来，JDK1.7 的链表结构就类似于上图情况下的二叉搜索树，当时数据元素节点较多的时候，查询速度很慢。JDK 1.8 采用红黑树，正是均衡了元素的增删性能问题，选择了性能均衡的红黑树，当链表节点元过多的时候，将数据结构转成红黑树，元素的查询性能得到提升。

4.2 HashMap 基本属性

HashMap 中的容器大小，默认扩容因子等都和 JDK 1.7 没有变化。在 JDK 1.8 中新增了对于红黑树相关的默认属性：

1
2
3
4
5
// 当链表中的元素个数超过 8 个时，链表转成红黑树
static final int TREEIFY_THRESHOLD = 8;

// 当链表中的元素个数小于 6 个时，红黑树转成链表
static final int UNTREEIFY_THRESHOLD = 6;

4.3 插入元素

4.3.1 hash 计算

在 JDK 1.8 中，对于 hash 值的运算比 JDK 1.7 更为简便一些，没有过多得算法，只是进行了将高 16 位和低 16 位进行了异或运算，此时相比 JDK1.7 的散列性要弱一些，因为红黑树的引用，所以不需要那么强的散列性。

1
2
3
4
static final int hash(Object key) {
    int h;
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}

4.3.2 插入元素源码分析

JDK 1.8 的源码的可读性没有 1.7 好，但是基本的思路和 1.7 是一致的。需要注意的是：新元素的节点是添加在链表的尾部。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node<K,V>[] tab; Node<K,V> p; int n, i;
    if ((tab = table) == null || (n = tab.length) == 0)
        // 初始化容器
        n = (tab = resize()).length;
    if ((p = tab[i = (n - 1) & hash]) == null)
        // 要插入的位置，没有元素，那么就直接插入到当前索引位置
        tab[i] = newNode(hash, key, value, null);
    else {
        Node<K,V> e; K k;
        if (p.hash == hash &&
            ((k = p.key) == key || (key != null && key.equals(k))))
           	// 当前的key 已经存在了
            e = p;
        else if (p instanceof TreeNode)
            // 当前要插入的节点是一颗红黑树，将新节点插入红黑树，如果已经存在，就返回该key所在红黑树节点
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else {
            // 遍历链表
            for (int binCount = 0; ; ++binCount) {
                // 直到遍历到链表的尾部
                if ((e = p.next) == null) {
                    // 插入新的节点到链表的尾部
                    p.next = newNode(hash, key, value, null);
                    // 检查此时的链表是不是需要转成红黑树
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);
                    break;
                }
                // 如果遍历的过程中，发现已经存在key了，直接跳出循环
                if (e.hash == hash &&
                    ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        if (e != null) { // existing mapping for key
            // 当前的key 已经存在了，更新value，返回旧的value
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e);
            return oldValue;
        }
    }
    ++modCount;
    if (++size > threshold)
        resize();
    afterNodeInsertion(evict);
    return null;
}

通过上面源码的注释可以看出，插入一个元素的时候一般分为三种情况：

  • 数组原本的位置为空
  • 数组原本的位置不为空，并且下面是链表的结构
  • 数组原本的位置不为空，并且下面是红黑树的结构

4.3.3 扩容时的 hash 计算

对原 key 的 hashCode 在扩容前后计算，会发现一些规律：

hashCode 中标红的位置如果为 1，那么扩容之后，其索引=原来索引值+原来容量大小，如果该位为 0，则索引值不变化。在 JDK 1.8 中将此规律应用了起来，在扩容方法resize()方法中就存在着此算法，因此没有重新计算 hashCode，减少了CPU资源开销。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table;
    int oldCap = (oldTab == null) ? 0 : oldTab.length;
    int oldThr = threshold;
    int newCap, newThr = 0;
    if (oldCap > 0) {
        // 原始表的容量大于最大限制了
        if (oldCap >= MAXIMUM_CAPACITY) {
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }
        // 原始表的容量没有超过最大限制，双倍扩容
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr;
    else {               // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) {
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr;
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
    table = newTab;
    if (oldTab != null) {
        // 遍历旧表的元素
        for (int j = 0; j < oldCap; ++j) {
            Node<K,V> e;
            if ((e = oldTab[j]) != null) {
                oldTab[j] = null;
                if (e.next == null)
                    // 旧表的索引位置，只有一个元素
                    newTab[e.hash & (newCap - 1)] = e;
                else if (e instanceof TreeNode)
                    // 红黑树拆分移动
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order
                    // 链表元素移动
                    Node<K,V> loHead = null, loTail = null;
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do {
                        next = e.next;
                        // 判断索引值要不要变化
                        if ((e.hash & oldCap) == 0) {
                            if (loTail == null)
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else {
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) {
                        loTail.next = null;
                        // 索引不变化
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        // 索引变化，加旧表的容量大小
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

因此，从上述分析和源码分析得出，在 JDK 1.8 中，旧表中的 hashCode 会转移到新表中，在新表中的位置索引值只有俩种可能：一种是原下标，另一种是原下标 + 旧表容量。

updated updated 2024-01-05 2024-01-05
本文结束感谢阅读

本文标题:浅析理解HashMap

本文作者:

微信公号:木鲸鱼 | woodwhales

原始链接:https://woodwhales.cn/2019/08/18/048/

许可协议: 署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。

0%