快速排序的俩种实现

算法描述

每一轮排序选择一个基准点（pivot）进行分区
1. 让小于基准点的元素的进入一个分区，大于基准点的元素的进入另一个分区
2. 当分区完成时，基准点元素的位置就是其最终位置
在子分区内重复以上过程，直至子分区元素个数少于等于 1，这体现的是分而治之的思想（divide-and-conquer）

从以上描述可以看出，一个关键在于分区算法，常见的有单边循环（洛穆托分区方案）、双边循环分区方案、霍尔分区方案

单边循环

核心思路

1，选择数组最右侧元素作为基准点

例如下图中的数组最右侧元素作为基准点。

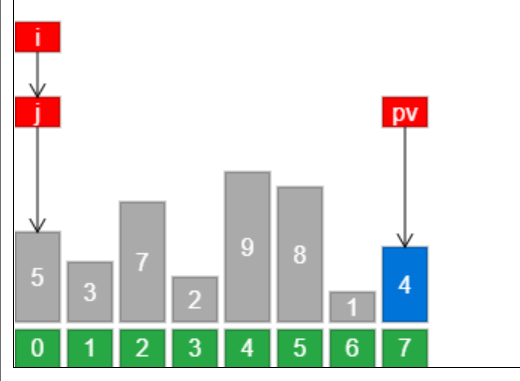
2，数组从左到右依次遍历元素，比基准点小的放置到基准点左边，比基准点大的放置到基准点右边

达到的效果如下图：

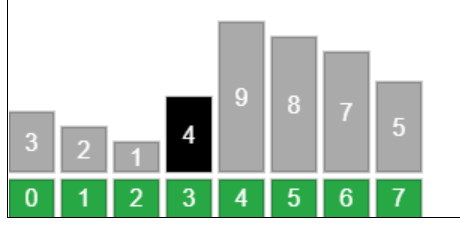
3，步骤 2 之后，基准点将原数组拆分成了俩个子集合。将俩个子集合看作新的集合，重复步骤1，2，直到子集合不能再拆分为止即可完成排序。

代码思路

如图示中，使用俩个游标初始值是数组的最左侧位置。

选择最右元素作为基准点元素
j 指针负责找到比基准点小的元素，一旦找到则与 i 进行交换，i++
i 指针维护小于基准点元素的边界，也是每次交换的目标索引
最后基准点与 i 交换，i 即为分区位置

代码实现

public class QuickSort1 {

    public static void main(String[] args) {
        int[] arr = {5, 3, 7, 2, 9, 8, 1, 4};
        System.out.println(Arrays.toString(arr));
        // 第一遍排序全数组
        quickSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    private static void quickSort(int[] arr, int low, int high) {
        // 地位大于等于高位则不需要进行排序，结束递归
        if(low >= high) {
            return;
        }
        // 完成第一遍，将数组按照基准点进行拆分，并得到基准点的索引位置
        int p = partition(arr, low, high);
        quickSort(arr, low, p - 1);
        quickSort(arr, p + 1, high);
    }

    private static int partition(int[] arr, int low, int high) {
        int pv = arr[high];

        int i = low;

        for (int j = low; j < high; j++) {
            if (arr[j] < pv) {
                swap(arr, i, j);
                i++;
            }
        }
        swap(arr, i, high);
        return i;
    }

    private static void swap(int[] arr, int i, int j) {
        if (i != j) {
            int temp = arr[i];
            arr[i] = arr[j];
            arr[j] = temp;
        }
    }
}

双边循环

核心思路

1，选择数组最左侧元素作为基准点

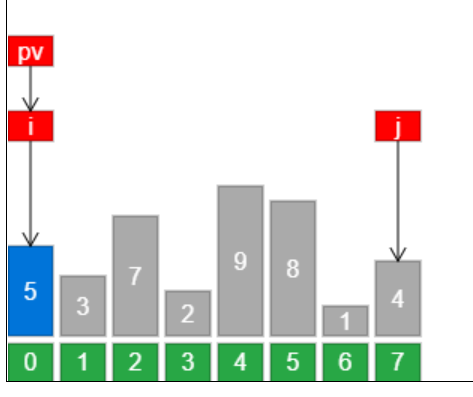
2，使用游标分别从数组的俩端往中间移动，左侧游标找比基准点小的，右侧游标找基准点大的，一旦找到就俩者游标对应的元素互换，直到俩个游标相遇为止。

3，俩个游标相遇的位置就是分区的位置。

代码思路

选择最左元素作为基准点元素
j 指针负责从右向左找比基准点小的元素，i 指针负责从左向右找比基准点大的元素，一旦找到二者交换，直至 i，j 相交
最后基准点与 i（此时 i 与 j 相等）交换，i 即为分区位置

要点

基准点在左边，并且要先 j 后 i
while( i **< j** && a[j] > pv ) j–
while ( i < j && a[i] <= pv ) i++

代码实现

public class QuickSort2 {

    public static void main(String[] args) {
        int[] arr = {5, 3, 7, 2, 9, 8, 1, 4};
        System.out.println(Arrays.toString(arr));
        // 第一遍排序全数组
        quickSort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    private static void quickSort(int[] arr, int low, int high) {
        // 地位大于等于高位则不需要进行排序，结束递归
        if(low >= high) {
            return;
        }
        // 完成第一遍，将数组按照基准点进行拆分，并得到基准点的索引位置
        int p = partition(arr, low, high);
        quickSort(arr, low, p - 1);
        quickSort(arr, p + 1, high);
    }

    private static int partition(int[] arr, int low, int high) {
        int pv = arr[low];

        int i = low;
        int j = high;
        while (i < j) {
            // 直到 arr[j] 小于等于基准点
            while (i < j && arr[j] > pv) {
                j--;
            }

            // 直到 arr[i] 大于基准点
            while (i < j && arr[i] <= pv) {
                i++;
            }
            // 上述俩个while循环保证了 i 和 j 一定会相遇，相遇则互换
            swap(arr, i, j);
        }

        // j 的位置就是分区索引位置
        swap(arr, low, j);
        return j;
    }
}